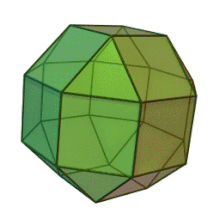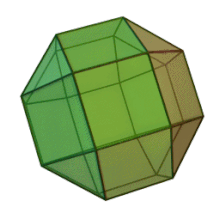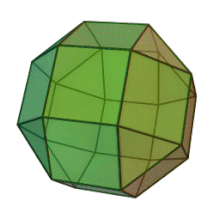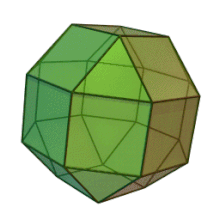
Petit rhombicuboctaèdre
Le petit rhombicuboctaèdre est un solide d'Archimède avec huit faces triangulaires et dix-huit faces carrées. Il possède 24 sommets identiques, avec un triangle et trois carrés s'y rencontrant[2]. Le polyèdre possède une symétrie octaédrique, comme le cube et l'octaèdre. Son dual est appelé l'icositétraèdre trapézoïdal, bien que ses faces ne soient pas réellement de vrais trapèzes.
| Faces | Arêtes | Sommets |
|---|---|---|
| 26 triangles et carrés | 48 | 24 de degré 4 |
| Type | Solide d'Archimède |
|---|---|
| Caractéristique | 2 |
| Propriétés | Semi-régulier et convexe |
| Volume (arête a) | |
| Aire de surface | |
| Groupe de symétrie | O |
| Dual | Icositétraèdre trapézoïdal |


Signification du nom
modifierLe nom rhombicuboctaèdre fait référence au fait que 12 des faces carrées sont placées dans les mêmes plans que les 12 faces du dodécaèdre rhombique qui est le dual du cuboctaèdre.
Il peut aussi être appelé un cube étendu ou un octaèdre étendu à partir des opérations de troncatures du polyèdre uniforme.
Données géométriques
modifierLes coordonnées cartésiennes pour un rhombicuboctaèdre sont toutes les permutations de
Il existe trois paires de plans parallèles qui coupent chacun le rhombicuboctaèdre à travers huit arêtes prenant la forme d'un octogone régulier. Le rhombicuboctaèdre peut être divisé le long de deux quelconques pour obtenir un prisme octogonal avec des faces régulières et deux polyèdres supplémentaires appelés coupoles octogonales, qui figurent parmi les solides de Johnson. Ceux-ci peuvent être rassemblés pour donner un nouveau solide appelé la bicoupole octogonale gyroallongée avec la symétrie d'un antiprisme carré. Dans celui-ci, les sommets sont tous localement les mêmes que ceux du rhombicuboctaèdre, avec un triangle et trois carrés se rencontrant à chaque sommet, mais ne sont pas tous identiques en ce qui concerne le polyèdre entier, puisque certains sont plus près de l'axe de symétrie que d'autres.
Il existe des distorsions du petit rhombicuboctaèdre telles que, alors que certaines faces ne sont pas des polygones réguliers, elles sont encore uniformes par les sommets. Certaines de celles-ci peuvent être faites en prenant un cube ou un octaèdre et en découpant les arêtes, puis en équilibrant les coins, ainsi le polyèdre résultant possède six carrés et douze faces rectangulaires. Celles-ci ont une symétrie octaédrique et forme une série continue entre le cube et l'octaèdre, analogue aux distorsions du petit rhombicosidodécaèdre ou des distorsions tétraédriques du cuboctaèdre. Néanmoins, le petit rhombicuboctaèdre possède aussi un deuxième ensemble de distorsions avec six faces rectangulaires et seize faces trapézoïdales, qui n'ont pas de symétrie octaédriques mais plutôt une symétrie Th, donc, ils sont invariants sous les mêmes rotations que le tétraèdre mais ont des réflexions différentes.
Les droites le long desquelles un Rubik's Cube peut être tourné sont, projetées sur une sphère, similaires, topologiquement identiques aux arêtes d'un petit rhombicuboctaèdre. En fait, les variantes utilisant le mécanisme du Rubik's Cube ont été produites, ressemblant de près au petit rhombicuboctaèdre.
Le petit rhombicuboctaèdre est un espace rempli par une combinaison de cubes et de tétraèdres.
Le rhombicuboctaèdre dans les arts
modifierDans le portrait de Luca Pacioli par Jacopo de' Barbari, le polyèdre suspendu, à gauche de l’image, est un petit rhombicuboctaèdre de verre à moitié rempli d'eau. Le dodécaèdre régulier en bas à droite est construit à partir d’un patron.
Le rhombicuboctaèdre de Michel Coignet est un cadran solaire[3] portatif en bronze construit au XVIe siècle.
Notes et références
modifier- Luca Pacioli, « De divina proportione », sur Bibliothèque de Genève.
- Six des carrés partagent seulement les sommets avec les triangles alors que les douze autres partagent une arête
- Connaissance des arts janvier 2014
Voir aussi
modifierArticles connexes
modifier- Le cube
- Le cuboctaèdre
- Le cube adouci
- L'octaèdre
- Le rhombicosidodécaèdre
- Le grand rhombicuboctaèdre
- La gyrobicoupole carrée allongée
- Le graphe rhombicuboctaédrique
- Le Rubik's Snake - Un puzzle qui peut former une "boule" rhombicuboctaédrique
Bibliographie
modifier- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979, (ISBN 0-486-23729-X)
Liens externes
modifier- (en) Archimède et le Rhombicuboctaèdre par Antonio Gutierrez de Geometry Step by Step from the Land of the Incas.
- (en) Les polyèdres uniformes
- (en) Les polyèdres en réalité virtuelle L'encyclopédie des Polyèdres
- (en) « SmallRhombicuboctahedron », sur mathworld.wolfram.com