Subdeterminant
V lineární algebře je subdeterminant nebo též minor matice determinantem podmatice, která byla z matice získána odstraněním některých řádků a sloupců. Počet řádků podmatice je řádem subdeterminantu. Subdeterminanty získané odstraněním právě jednoho řádku a jednoho sloupce ze čtvercové matice umožňují redukovat řád determinantu pomocí rozvoje podle řádku nebo sloupce. Prostřednictvím adjungované matice také souvisejí s inverzní maticí.
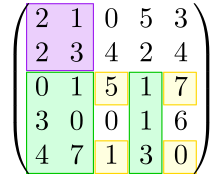
Definice
editovatPro matici typu a se subdeterminantem nebo minorem řádu , nazývá determinant čtvercové matice řádu získané z matice odebráním řádků a sloupců. Někdy se používá slovo „stupeň“ pro „řád“ subdeterminantu či minoru. Termín „minor“ se také nesprávně používá k označení čtvercové matice řádu získané uvedeným způsobem, ale tato matice by měla být označována jako (čtvercová) podmatice matice , přičemž výraz „minor“ by měl být užíván pouze pro determinant této matice.
Matice typu má celkem subdeterminantů řádu . Subdeterminant řádu nula je definován jako 1.
Operace odebrání formálně spočívá ve výběru posloupnosti indexů řádků a posloupnosti indexů sloupců . Tyto vybrané množiny indexů a se použijí k výpočtu determinantu podmatice , čili výrazu:
Je-li čtvercová matice řádu , potom její první minor je každý subdeterminant řádu , a jako takový vzniká odebráním jednoho řádku a sloupce. Podobně pro druhé a další minory. Za nultý minor čtvercové matice lze považovat její determinant.
První minor, který je determinantem podmatice vytvořené z čtvercové matice odstraněním -tého řádku a -tého sloupce se nazývá subdeterminant (minor) příslušný k prvku matice .
Pokud , čili pokud z matice bylo ponecháno řádků a sloupců se stejnými indexy, nazývá se odpovídající subdeterminant hlavním minorem stupně (platí i pro obdélníkové matice). Hlavní minor stupně , vzniklý odebráním posledních řádků a sloupců, neboli daný množinami se nazývá vedoucí hlavní minor řádu . U čtvercových matic řádu se nazývá též -tý vedoucí (hlavní) minor.
Někdy jsou vedoucí hlavní minory nazývány hlavními minory, zatímco první zmíněné nejsou nijak zvlášť pojmenovány.
Ukázka
editovatU reálné matice
typu vznikne odebráním druhého řádku a také druhého a třetího sloupce, neboli ponecháním prvků s řádkovými indexy z množiny a sloupcovými indexy z množiny subdeterminant hodnoty:
Tento minor není hlavní, protože . Hlavní minor matice je například subdeterminant
odvozený z množin .
Vedoucí hlavní minory matice jsou:
- řádu 1: řádu 2: řádu 3:
Subdeterminant příslušný k prvku reálné čtvercové matice
je roven:
Použití subdeterminantů
editovatAlgebraický doplněk
editovatAlgebraickým doplňkem nebo také kofaktorem prvku čtvercové matice nazýváme číslo
kde je subdeterminant příslušný k prvku matice . Transponovaná matice z algebraických doplňků se nazývá adjungovaná matice. Adjungovaná matice k regulární matici je -násobkem její inverzní matice.
Laplaceův rozvoj determinantu
editovatAlgebraický doplněk lze použít k výpočtu determinantu. Pro libovolný (pevně daný) řádkový index lze determinant matice řádu vyjádřit pomocí součtu součinů všech prvků tohoto řádku a jejich algebraických doplňků:
- .
Tento vzorec se nazývá (Laplaceův) rozvoj (rozklad) determinantu podle -tého řádku. Vzhledem k tomu, že se determinant nezmění transpozicí matice, lze jej vyjádřit teké rozvojem (rozkladem) podle -tého sloupce:
- .
Pomocí těchto vzorců lze výpočet determinantu převést na výpočet několika subdeterminantů, jejichž řád je o jedna menší. Opakováním tohoto procesu lze dospět až k subdeterminantům prvního řádu, jejichž hodnota je odpovídá jednotlivým prvkům matice. Uvedený postup vede na rekurentní algoritmus pro výpočet determinantu. Navzdory jednoduché implementaci roste jeho výpočetní složitost exponenciálně rychle s řádem determinantu, proto je vhodnější determínant počítat např. Gaussovou eliminační metodou.
Rozvoj determinantu je možné zobecnit[1] i na rozvoj podle víceprvkové množiny vybraných řádků s využitím všech možných subdeterminantů sestavených z těchto řádků.
Další aplikace
editovatKaždá reálná matice typu hodnosti (platí i pro matice nad libovolným tělesem) má alespoň jeden nenulový subdeterminant řádu , zatímco všechny subdeterminanty řádu alespoň jsou nulové.
U hermitovských matic mohou být vedoucí hlavní minory použity k testu pozitivní definitnosti podle Sylvesterova kritéria a hlavní minory mohou být podobně použity k testu pozitivní semidefinitnosti.
Jak vzorec pro obyčejný součin matic, tak i Cauchyho–Binetův vzorec pro determinant součinu matic jsou speciálními případy následujícího obecného tvrzení o subdeterminantech součinu matic. Jsou-li matice typu , matice typu a jsou-li a dvě -prvkové podmnožiny množin a , potom platí:
- ,
kde součet prochází přes všechny -prvkové podmnožiny množiny . Uvedený vztah je přímým rozšířením Cauchyho–Binetova vzorce.
Odkazy
editovatReference
editovatV tomto článku byly použity překlady textů z článků Minor (linear algebra) na anglické Wikipedii, Minor (Lineare Algebra) na německé Wikipedii a Minor na polské Wikipedii.
- ↑ HORÁK, Pavel; JANYŠKA, Josef. Lineární algebra [online]. Masarykova Univerzita [cit. 2022-06-04]. S. 34. Dostupné online.
Literatura
editovat- BÄRTSCH, Hans-Jochen. Matematické vzorce. Praha: Academia, 2006. 832 s. ISBN 80-200-1448-9. Kapitola Matice, s. 180–198.
- BEČVÁŘ, Jindřich. Lineární algebra. 1.. vyd. Praha: Matfyzpress, 2019. 436 s. ISBN 978-80-7378-392-1.
- HLADÍK, Milan. Lineární algebra (nejen) pro informatiky. 1.. vyd. Praha: Matfyzpress, 2019. 328 s. ISBN 978-80-7378-378-5. S. 39.
- OLŠÁK, Petr. Lineární algebra [online]. Praha: 2007 [cit. 2023-02-20]. Dostupné online.
- MOTL, Luboš; ZAHRADNÍK, Miloš. Pěstujeme lineární algebru [online]. [cit. 2023-02-20]. Dostupné online.
