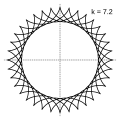
Hipocicloide
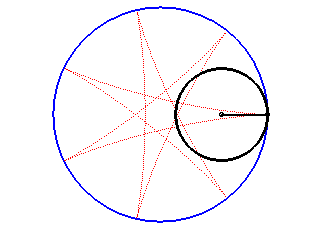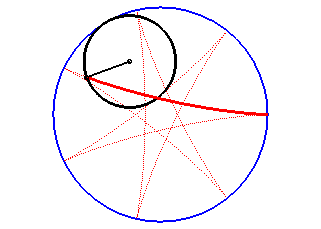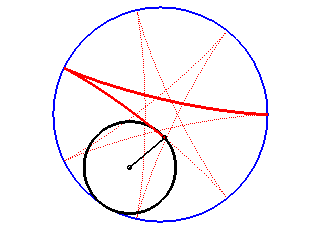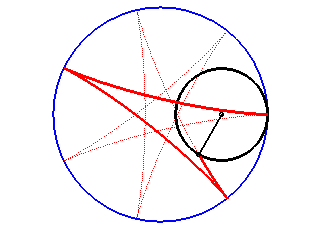
Una hipocicloide és una corba plana transcendint, que és la trajectòria d'un punt fixat en una circumferència que roda sense lliscar sobre una altra circumferència anomenada directriu i dins d'aquesta. Es tracta per tant d'un cas particular de corba cicloïdal.
Etimologia i història
modificaLa paraula és una extensió de cicloide, inventada el 1599 per Galileo Galilei, i té la mateixa etimologia: ve del grec hupo (sota), kuklos (cercle, roda) i eidos (forma, «semblant a»).
La corba mateixa va ser estudiada per Albrecht Dürer el 1525, Rømer el 1674 (que la va batejar) i Daniel Bernoulli el 1725.
Definició matemàtica
modificaUna hipocicloide pot ser definida per l'equació paramètrica següent:
on és el radi de la circumferència de base i el de la circumferència rodant. Amb , per tant aquesta equació també es pot escriure:
Definició en el pla complex
modificaPot ser útil passar en notació complexa, i s'obté l'equació següent:
Si es desitja a més fer intervenir el temps t per expressar la velocitat a la qual es descriu el moviment, cal introduir les dues velocitats angulars
La coordenada complexa del centre de la circumferència petita és simplement i la d'un punt de la circumferència petita respecte al seu centre . La suma d'aquests dos nombres complexos dona llavors la coordenada complexa d'un punt de la circumferència petita respecte al centre de la gran.
Així i més generalment, es pot definir una hipocicloide per la seva equació en el pla complex:
En efecte la condició expressa la igualtat de les longituds dels arcs de les circumferències petita i gran recorreguts durant el temps t pel punt de contacte i per tant indica que la circumferència petita no llisca en la seva rotació al si de la gran. Per això quan un punt de la circumferència petita, és a dir de la hipocicloide, entra en contacte amb la gran, la seva velocitat és nul·la la qual cosa correspon a un punt de retrocés.
Finalment, s'observa que la definició de l'equació (3) pot ser interpretada geomètricament d'una altra manera (propietat de la doble generació) basant-se en la propietat commutativa de la suma de dos vectors i que la hipocicloide és també la suma d'un petit moviment circular al qual s'afegeix un gran moviment circular en sentit oposat .
Propietats
modificaLa corba està formada per arcs isomètrics (anomenats arcs) separats per punts de retrocés. Si q és racional (i es pot per tant escriure q=a/b on a i b són enters), a representa el nombre d'arcs de la corba. També es poden veure aquestes dues magnituds de la manera següent:
- a representa el nombre de rotacions de la circumferència que roda necessàries per portar el punt mòbil a la seva posició de sortida
- b representa el nombre de voltes de la circumferència base necessàries a la circumferència que roda per tornar al punt de sortida.
Els punts de retrocessos s'obtenen per . La longitud d'un arc és de .
Si q és enter, la longitud total de la corba val vegades la longitud de la circumferència base, i l'àrea total val vegades la de la circumferència base.
El teorema de la doble generació prova que una hipocicloide és també una pericicloïde, és a dir la corba descrita per un punt d'una circumferència de radi r+R rodant sense lliscar sobre aquesta circumferència directora al continent.
Les petites oscil·lacions del pèndol de Foucault formen també una hipocicloide.
Vegeu també
modifica- Quan el punt mòbil no està fixat sobre la circumferència que roda sinó a l'exterior o l'interior d'aquesta es parla llavors de hypotrocoide, que és un cas particular de trocoide. D'altra banda, l'espirògraf realitza hypotrocoides.
- Quan la circumferència mòbil gira fora de la circumferència directriu, la corba dibuixada s'anomena llavors epicicloide.
- Si R = 2r, la hipocicloide és un diàmetre de la circumferència base (vegeu el Teorema de La Hire).
- Si R = 3r, la hipocicloide és una deltoide. S'obté una figura idèntica si R = 3/2 x r. en Aquest Cas, es tracta també de l'envolvent del diàmetre de la circumferència que roda.
- Si R = 4r, la hipocicloide és una astroide. Obtenim, doncs, una figura idèntica si R = 4/3 x r. En aquest cas, es tracta igualment de l'envolvent del segment de llargada constant R en el qual les extremitats descriuen els eixos d'una referència ortonormal.
Bibliografia
modifica- Marcel Berger, Géométrie (Tomo 1).
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, ISBN 978-2-91-635208-4
- Petite encyclopédie de mathématique (Ed. Didier)
- Méthodes modernes en géométrie de Jean Fresnel